Training deep networks requires careful initialization. If weights are too small, activations and gradients can shrink toward zero; if too large, they can grow out of control. Also known as the Glorot Initialization, the Xavier Initialization was proposed by Xavier Glorot and Yoshua Bengio in 2010. It is designed to combat both, vanishing and exploding gradient problems during the training of deep neural networks. Particularly, when using activation functions like tanh and logistic sigmoid.

Variance Preservation: Two conflicting goals

The Xavier Initialization engineers a compromise between two conflicting goals:

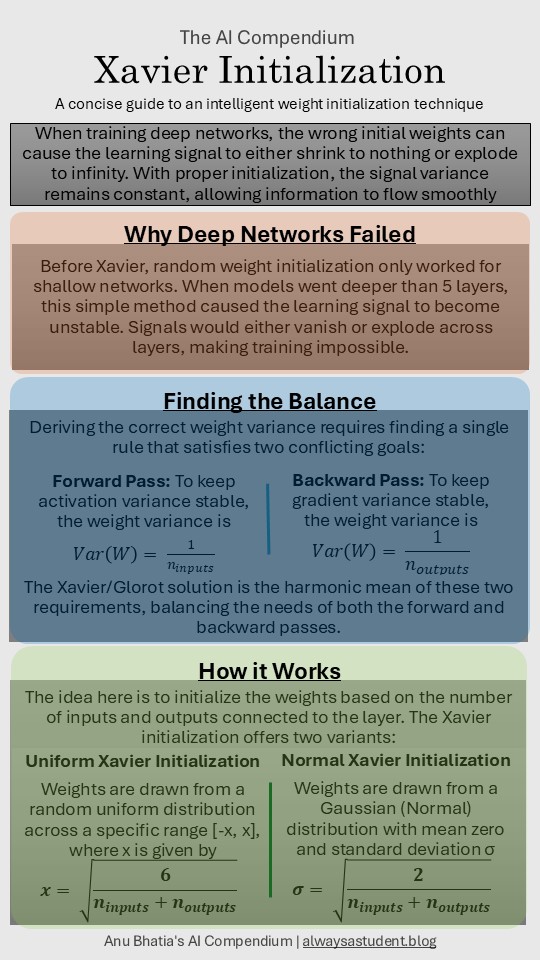
1. Preserving Activation Variance: In order to ensure that the variance of the activation outputs remain stable during the forward pass, the variance of the weights should be equal to the reciprocal of the number of inputs.
2. Preserving Gradient Variance: In order to ensure that the variance of the gradients remains stable during back-propagation, the variance of the weights should be equal to the reciprocal of the number of outputs.

How it Works

The core idea of the Xavier Initialization is to initialize the weights based on the size of the layer they are connecting. The weights are drawn from a distribution whose variance is dependent on the number of input unit (n_inputs) and output units (n_outputs) of the layer. This initialization method offers two variants with which the weights can be initialized:

• Uniform Xavier Initialization
  • Here, the weights are drawn from a random uniform distribution across a specific range
  • The range is [-x,x], where x is defined as

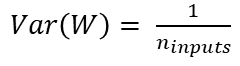
• Normal Xavier Initialization
  • Here, the weights are drawn from a Gaussian (normal) distribution with a mean of 0 and a specific standard deviation given by

Xavier initialization provides a mechanism to scale weights appropriately for the network’s topology.